A diszperzió a diszperzió képletű, a fajta a diszperzió, egy egyszerű diszperziója a súlyozott szórásnégyzet
A koncepció a diszperziós
A variancia a statisztikában az átlagos négyzetes eltérés az egyes jellemző értékek a négyzet a számtani átlaga. Attól függően, hogy a kezdeti adatok meghatározása egyszerű képletek és a súlyozott varianciák:
1. Egyszerű diszperziós (a csoportosított adatok) képlettel számítottuk ki:
2. A súlyozott variancia (számos változatban):
ahol n - a frekvencia (ismételhetőség X faktor)
Példa diszperziós megállapítás
Ezen az oldalon megismerheti a szabványos példája a megállapítás a diszperziós, akkor is látni más feladatokat a megállapítását
1. példa Az alábbi adatok egy csoportja 20 diák a levelezés osztály. Ki kell építeni több olyan jellegzetes intervallum forgalmazás, számítsuk ki az átlagos értéke a jel és megvizsgálja annak diszperziós
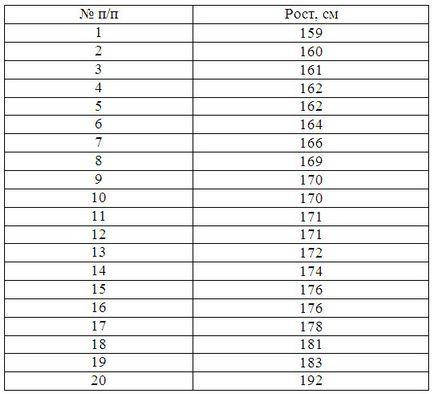
ahol X MAX maximális csoportosítás funkció;
X min-minimum érték csoportosítás funkció;
N - intervallumok számát:
Fogadunk n = 5. Lépés egyenlő: h = (192-159) / 5 = 6,6
Forma intervallum csoport
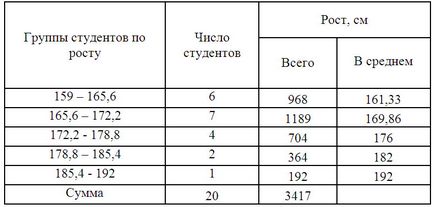
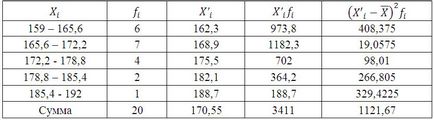
Az átlagos értéke a diákok növekedés, amelyet a képlet súlyozott átlag:
Definiáljuk a diszperziót a következő képlet szerint:
diszperziós képletű átírható a következőképpen:
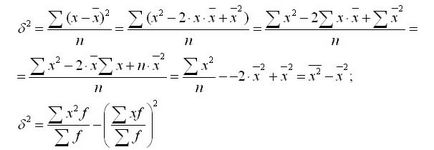
Ebből a képletből következik, hogy a diszperziós közeg egyenlő a különbség a terek és egy négyzet kiviteli alak és az átlagos.
Diszperzió variációs sorokban egyenlő időközönként módszer szerint a pillanatok következő módszerrel lehet kiszámítani a második diszperziós tulajdonságokat (elosztjuk az összes variációk a nagysága a intervallum). Meghatározása a szórás. által kiszámított momentumok módszerével, az alábbi képlet kevésbé munkaigényes:
ahol i - az érték az intervallum;
A - névleges nulla kényelmesen használható középső intervallumot, amely a legnagyobb gyakorisággal;
m1 - négyzet pontok az elsőrendű;
m2 - másodrendű pillanat
A diszperzió alternatív jel (ha a statisztikai populáció megjelölés úgy változik, hogy csak két kölcsönösen kizárólagos kiviteli, az ilyen változékonyság úgynevezett alternatív) lehet képlettel számítottuk ki:
Behelyettesítve ezt a diszperziót képletű q = 1- p, kapjuk:
diszperziós típusú
A teljes variancia méri változása jellemző az egész populáció egészére hatása alatt valamennyi tényező felelős a variáció. Ez egyenlő átlagos négyzetes eltérései az egyes értékek a jellemző x teljes átlagos értéke az x és lehet meghatározni, mint egy egyszerű diszperziót vagy a súlyozott variancia.
A csoporton belüli variancia jellemzi a véletlen variáció, azaz A variáció, amely által okozott hatása rögzítetlen tényezők, és nem függ a jellemző faktort, fekvő csoportosításában bázis. Ilyen variancia az átlagos négyzetes hiba értékeket külön jellemző a csoporton belül X a számtani átlaga a csoport, és ki lehet számítani, mint egyszerű, mint egy súlyozott variancia vagy diszperzió.
Így, intra-diszperzió jellemző intézkedések a variáció a csoporton belül és adja meg:
ahol xi - a csoport átlagos;
ni - az egységek száma a csoportban.
Például, a csoporton belüli variancia, amelyet meg kell határozni a feladat hatásait tanulmányozzuk a munkavállalók készségeinek szintjét munka termelékenysége az üzlet show változatait kimenet mindegyik csoportban okozta az összes lehetséges tényezőt (műszaki berendezések állapotának, nyújtása eszközöket és anyagokat, a kor a munkások, munkaerő-intenzitása stb .) foglalt eltérésekkel az időmérő mentesítés (a csoporton belül minden munkavállalónak ugyanolyan végzettséggel).
Átlagos csoporton belüli variancia tükrözi a véletlenszerű variáció. T. E. Tu része a variáció, hogy történt hatása alatt a más tényezők, kivéve a csoport faktor. Ez a következőképpen számítjuk ki:
Intergroup diszperzió jellemzi szisztematikus variációs kapott változót, amely által okozott a befolyása a funkció faktor, fekvő csoportosításában bázis. Ez egyenlő a közepes négyzetes eltérés a csoport átlagok a teljes átlag. Két-csoport variancia a következőképpen számítjuk ki:
Jellemzően a hozzáadott diszperzió statisztika
A szabály szerint hozzáadás varianciák összes változás az összege az átlagos belüli és a csoportok közötti variancia:
A lényeg ez a szabály, hogy a teljes diszperziós, amely akkor hatása alatt valamennyi tényező összege szórások fordulnak elő hatása alatt az összes többi tényező, és a diszperziós fordul elő, hogy csoportosításával tényező.
A képlet diszperziók felül lehet meghatározni két ismert diszperziók harmadik ismeretlen, és a bíró a ütésállóság csoportosulás funkciót.
diszperziós tulajdonságokkal
1. Ha az összes jellemző érték csökkenése (növekedése) ugyanaz a konstans értéket, akkor a szórás nem változik.
2. Ha az összes értékek funkció csökkenése (növekedése) azonos számú alkalommal n, a diszperzió megfelelően csökken (növekedése) n ^ 2-szer.