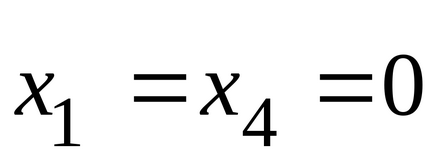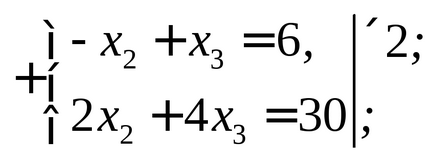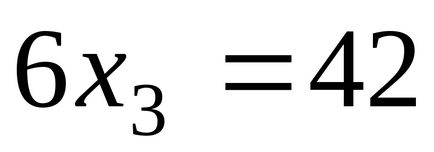Általános szabályok kidolgozásához két problémát

1. szabály: minden korlátozás az eredeti probléma ingyenes tagok legyen a jobb oldalon, és a tagok számára ismeretlen - a bal oldalon.

2. szabály: a kezdeti probléma kényszerek-egyenlőtlenségeket kell írni, hogy az egyenlőtlenség jelei voltak ugyanabban az irányban.

Szabály 3. Ha az egyenlőtlenséget jelek a megszorítások az eredeti probléma "

„A célfüggvény, és ha”„Akkor.

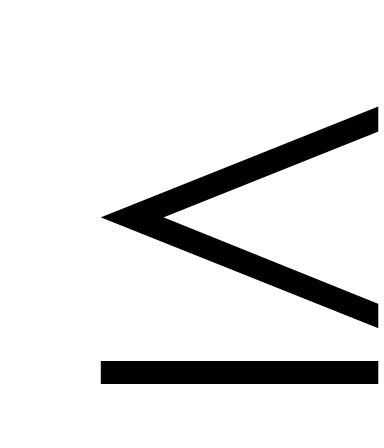
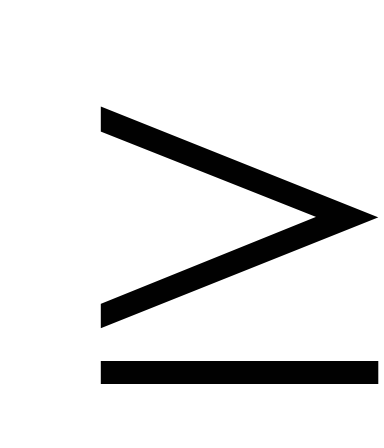
4. szabály minden korlátozás ismeretlen forrásból probléma megfelel a kettős probléma, az ismeretlen megfelelő restrikciós-egyenlőtlenség meg kell felelniük a feltétel nem negativitás és ismeretlen megfelelő egyenlőség korlátok lehetnek akár jel.

5. szabály A célfüggvény a kettős probléma formájában

,

ahol

- ingyenes kifejezéseket a megszorítások az eredeti probléma.

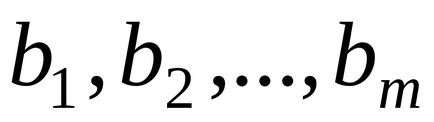
6. szabály: A célfüggvény

Meg kell optimalizálni képest az ellenkezőmódon.

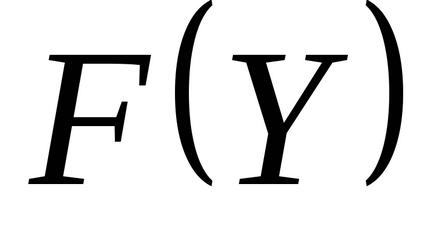
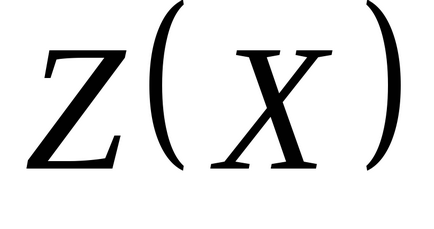
Szabály 7. Mindegyik neizvestnomuhj, j = 1, 2, ..., n az eredeti probléma korlátnak megfelelő a kettős problémát. A korlátozás készletet etihn (együtt nem-negativitás neizvestnyhyi körülmények között. Egyenlőtlenségei-releváns korlátait az eredeti probléma) egy olyan rendszert képez korlátai kettős probléma. Minden megszorítások a kettős probléma van formájában egyenlőtlenségek, ingyenes tagok, akik a jobb oldalon, és tagjaival neizvestnymiy1, y2. ...,

- a bal oldalon.

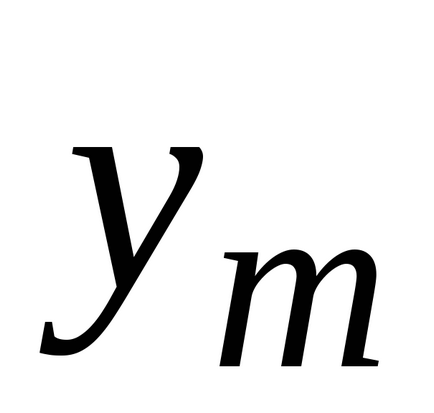
Minden egyenlőtlenség jelek a forma "

„Ha, és”„Akkor.

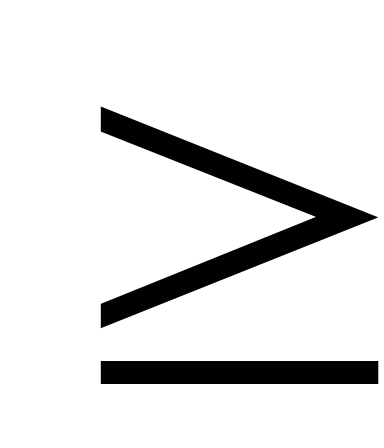
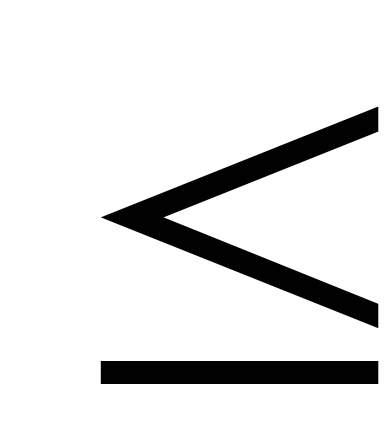
6.2. Egyidejű előállítása az ősi és a kettős probléma

Egyidejű előállítása az ősi és a kettős probléma alapja az elmélet a kettősség. A dualitás tételek teszi számunkra, hogy hozzon létre kapcsolatát az optimális megoldás egy pár két problémát. Döntés az egyik egy pár két problémát, vagy megtalálja az optimális megoldást egy másik probléma, nem oldja meg, vagy állítsa a hiányát. Az alábbi esetekben:

- mindkét probléma a kettős párok optimális megoldást;

- Az egyik probléma az, nincs megoldás a szem elől a célfüggvény nem korlátos, és a másik nincs megoldás, tekintettel a összeférhetetlenségét rendszer korlátait.

Tétel 6.2.1 (1. dualitás). Ha egyik célkitűzése a kettős pár kölcsönösen oldódnak, az megoldható és egyéb tárgyak, ebben az esetben az optimális értékek a cél funkciók azonosak. Ha az objektív függvény egyik célkitűzése nem korlátozódik (top -, hogy maximalizálja a probléma alulról - annak érdekében, hogy minimálisra csökkentsék a probléma), a készlet megvalósítható tervek egyéb feladatok üres.

Ez a tétel magában foglalja a következő

Következmény. Annak érdekében, hogy megvalósítható megoldásokat

ésduális pár problémák optimális, szükséges és elégséges, hogy az objektív függvény a következő síkok egybeesnek:.

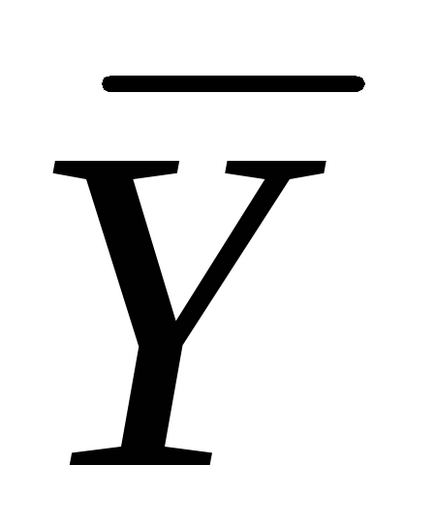
Tétel 6.2.2 (2. dualitás). Legyen szimmetrikus pár kettős problémák

, ;,.

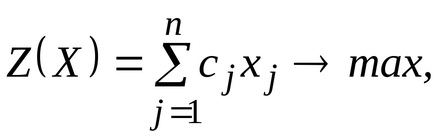
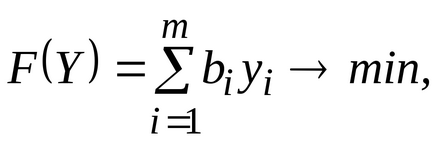
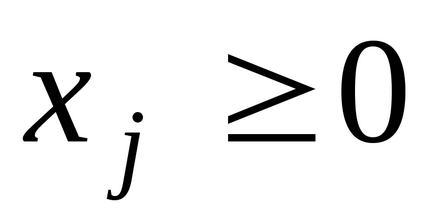
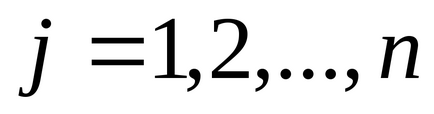
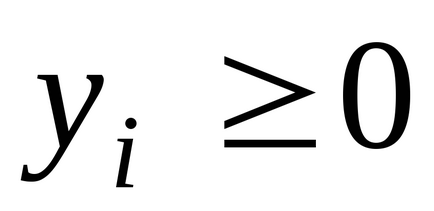
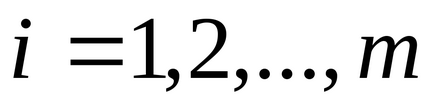
Annak érdekében, hogy megvalósítható megoldásokat, az optimális megoldás pár kettős probléma, szükséges és elégséges, hogy az alábbi egyenletek:

Ellenkező esetben, ha a helyettesítés az optimális megoldás az i-edik korlátozások korlátozza a kezdeti feladatot, mint egy szigorú egyenlőtlenség, TOI-koordinátája az optimális megoldás a kettős probléma nulla, és fordítva, eslii koordinátája az optimális megoldás a kettős problémát nullától eltérő, toi- azaz korlátozza a kezdeti probléma az optimális megoldás elégedett, mint az egyenlőség.

6.2 példa. Ezt a problémát, hogy egy kettős megoldani a grafikus eljárással, a második dualitás, hogy megoldást találjanak az eredeti probléma:

, .

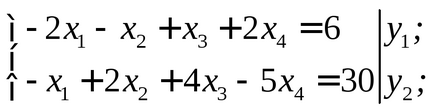
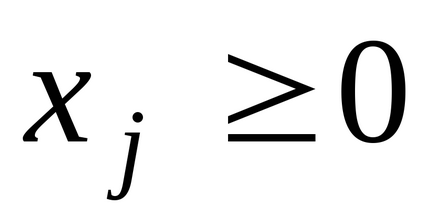
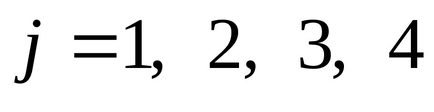
Határozat. Építünk kettős problémájának

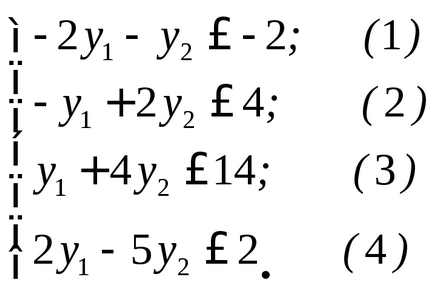
Mi megoldjuk ezt a problémát, grafikus módszerrel. Ábra. A 6. ábra a különböző megengedett megoldások a probléma, a normális

szintvonalakat, szintvonalakat és optimális megoldás.

,

;

, ;

;

.

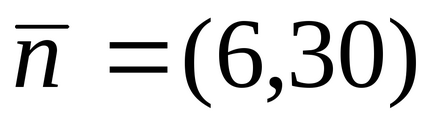
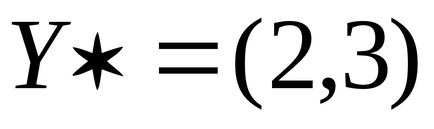
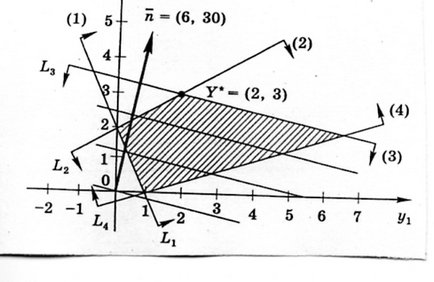
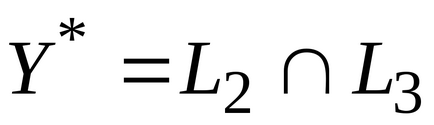
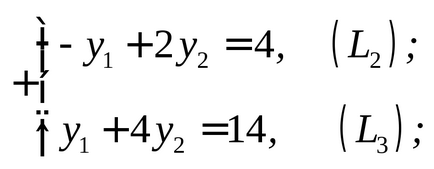
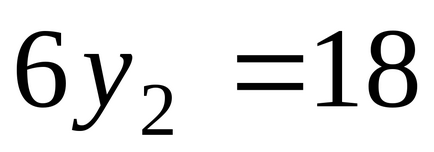
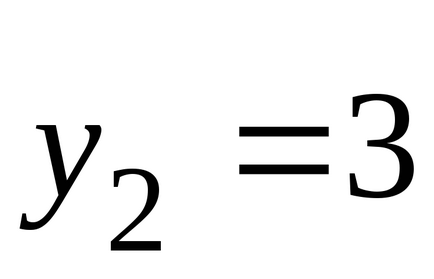
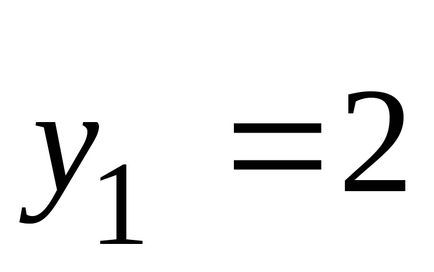
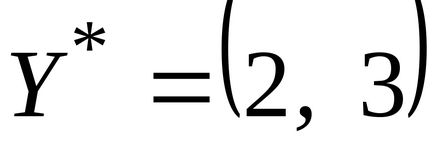
Helyettesítsük az optimális megoldás

korlátozását. Azt látjuk, hogy korlátozások (1) és (4) hajtja végre a szigorú egyenlőtlenség:

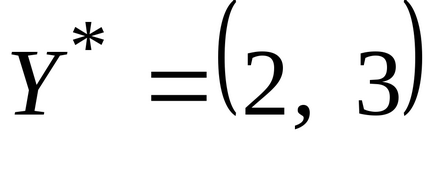
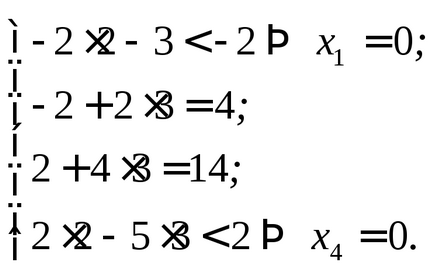
Szerint a második dualitás a megfelelő koordinátáit az optimális duál megoldás, azaz, Az eredeti probléma nulla:

. Ezt szem előtt tartva, az eredeti probléma a rendszer korlátaira kap

;