Azonosítás és tulajdonságait a prizma
A fő vizsgálat tárgya szilárd geometria helyet szervek. A test a része által határolt térben egy felületet.
Polyhedron nevezzük test, amelynek a felületi áll véges számú sík sokszög. A poliéder konvex, ha található egyik oldalán a sík minden egyes sík poligon a felületén. Az általános rész a sík és a felület a poliéder nevezzük egy arc. Metszettel lapos konvex poliéder konvex sokszög. Oldalán az úgynevezett poliéder élei. és a felső - poliéder.
Például, egy kocka áll hat négyzetek annak oldalait. Éleket tartalmaz, amely 12 (oldalsó négyzetek) és 8 csúcsa (a csúcsai a négyzetek).
Egy egyszerű poliéder prizma és egy piramis, hogy a tanulmány és részt.
Azonosítás és tulajdonságait a prizma
Polyhedron nevezzük prizma, amely két sík sokszög fekvő párhuzamos síkokban egymás fölött elhelyezett párhuzamos fordítás, és az összes a szegmensek összekötő megfelelő pontok ezen sokszögek. A sokszögek nevezzük a bázisok a prizma. és a szegmensek összekötő megfelelő csúcsokat a sokszögek, - oldalsó bordák a prizma.
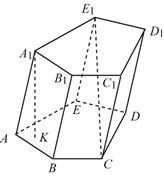
A magassága a prizma közötti távolság a síkok a bázisok (). Két részletét kapcsolja össze vertex prizmák, nem tartozó egyik oldalán, az úgynevezett átlós prizma (). Prism nevezzük n szögű. ha bázisként n-gon.
Bármilyen prizma a következő tulajdonságokkal rendelkezik a következő a tény, hogy a prizma bázist párhuzamosan állnak fordítás:
1. alapja a prizma egyenlő.
2. Az oldalsó prizma élei párhuzamosak és egyenlő.
A felület a prizma áll bázisok és az oldalfelület. Az oldalsó felülete a prizma áll egy paralelogramma (ez következik a tulajdonságok a prizma). Területe az oldalsó felület a prizma a területek összege az oldalsó felületek.
Prism hívják közvetlen. ha az oldalsó élei mentén merőleges a szubsztrátok. Egyébként ez az úgynevezett ferde hasáb.
Egyenes hasáb arcok téglalapok. A magasság az egyenes hasáb egyenlő oldalfelületén.
Teljes felülete az összege a prizma oldalsó felületek és bázisok.
Jobb hasáb nevezzük egyenes hasáb szabályos sokszög a földbe.
Tétel 13.1. A terület a palástfelület egy egyenes hasáb egyenlő a termék a kerülete a prizma magassága (vagy ezzel ekvivalens, a oldaléle).
Bizonyítás. Oldalfelületeinek egyenes hasáb van téglalapok bázisokat tartalmazó felek poligonok a prizma szubsztrátok, és a magasság az oldalsó bordák a prizma. Aztán, definíció szerint, az oldalsó felület:
ahol - a bázis kerülete egyenes hasáb.
Ha az alap a hasáb paralelogramma, ez az úgynevezett téglatest. Minden részletét a doboz - paralelogramma. Ebben az esetben a homlokfal a doboz párhuzamosak és egyenlő.
Tétel 13.2. téglatest átlói metszik egy ponton, és a metszéspont kettéváló.
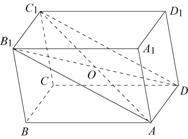
Bizonyítás. Tekintsünk két tetszőleges átló, például, és. mert az arcok a téglatest a paralelogramma, akkor. és így tovább T két párhuzamos egyenesek egy harmadik. Ezen túlmenően, ez azt jelenti, hogy a közvetlen és a hazugság egy síkban (a gépet). Ez a sík metszi a sík párhuzamos és egyenesek és párhuzamosak. Így a négyszög - paralelogramma, és egy paralelogramma az ingatlan, és annak átlói metszik és a metszéspont vannak osztva a felére, ha szükséges.
Közvetlen téglatest, amelynek alapja a téglalap hívják hasáb alakú. Minden részletét egy téglatest - téglalapok. A hossza nem párhuzamos élei egy derékszögű paralelepipedon nevezzük annak lineáris méretei (méretek). Az ilyen három dimenzióban (szélesség, magasság, hosszúság).
Tétel 13.3. A derékszögű paralelepipedon négyzet bármely átlós egyenlő a négyzetének összege a három dimenzió (bizonyult révén két-szeres alkalmazása Pythagoras T).
Téglatest, amelynek során valamennyi élek nevezzük kocka.
13.1Skolko diagonális prizma van n -ugolnaya
13.2V ferde háromszög prizmához távolság az oldalélek között 37 egyenlő, a 13. és a 40. Find közötti távolság nagyobb oldalfelületen, és a szemközti oldalsó szélét.
13.3Cherez oldali alsó bázis szabályos háromszögű hasáb lefolytatott metsző síkban oldalfelületeinek a szegmensek, a köztük lévő szög. Keresse meg a hajlásszöge a gépet, hogy az alap a prizma.
13.4Storona bázis szabályos négyszögletes hasáb 15, magasság: 20. Keresse meg a legrövidebb távolság a bázis oldalán nem metsző átlója prizma.
13.5Ploskost áthaladó oldalán az alap szabályos háromszögű hasáb és a középpontját a szemközti borda szöget zár be az alap 45 a. Az alsó oldalon egyenlő. Keresse oldalsó felületén a prizma.
13.6Bokovoe téglatest borda van 5, a bázis oldalán -6, és a 8. és az egyik átlója a bázis - 12. megtalálják átlós a paralelepipedon.
13.7Rebro kocka egyébként. Keresse meg a távolságot a tetején a kocka átlók összeköti a két másik csúcs.
13.8Diagonali három téglatest konvergáló csúcsán egyenlő. és. Keresse meg a lineáris méretei a doboz.
13.9Dokazat, hogy a kocka átlós síkjára merőleges.
13.10 Arcok a kocka egyenlő. Keresse meg a távolságot a ferdeség és az átlók a kocka.