Hogyan lehet megtalálni a terület a palástja piramis
Először is, meg kell értenünk, hogy az oldalsó felület a piramis által képviselt több háromszög, a terület, amely megtalálható a különféle képletek, attól függően, hogy az ismert adatok:
S = (a * h) / 2, ahol h - magasság, esett oldalán egy;
S = a * b * sinβ, ahol a, b - oldalán a háromszög, és a β - közötti szög ezek a felek;
S = (r * (a + b + c)) / 2, ahol a, b, c - oldalán a háromszög, és r - sugara a háromszög beírt egy kört;
S = (a * b * c) / 4 * R, ahol R - a kör sugara körül a háromszög;
S = (a * b) / 2 = R + 2 * r * R (ha háromszög - téglalap alakú);
S = S = (a² * √3) / 4 (ha háromszög - egyenlő oldalú).
Tény, hogy ez csak a legalapvetőbb, a jól ismert képletek megtalálásához háromszög területe.
Számított a fenti képlet alapján területének az összes háromszögek az arcok a piramis, akkor folytassa a számítás a terület az oldalsó felületén a piramis. Ez nagyon egyszerűvé válik: add ki a területen az összes háromszöget alkotnak az oldalsó felületén a piramis. Ez a képlet lehet kifejezni:
Sn = ΣSi, ahol az SN - az oldalsó felülete a piramis, Si - i-edik háromszög területe, amely része oldalsó felületén.
Az érthetőség kedvéért, az egyik figyelembe lehet venni egy kis példát adott szabályos piramis, oldalfelületeinek amelyek által alkotott egyenlő oldalú háromszög, és ez fekszik a bázis a tér. A hossza a bordák a piramis 17 cm. Van szükség, hogy megtalálják a terület az oldalsó felületén a piramis.
Megoldás: Az ismert hossza szélén a piramisok, azt tudjuk, hogy előtte -, egyenlő oldalú háromszög. Így azt mondhatjuk, hogy minden oldalról az összes háromszög egyenlő az oldalirányú felületét 17 cm Ezért, annak érdekében, hogy kiszámítható a terület minden ilyen háromszög alkalmazniuk kell a képlet .:
S = (17² * √3) / 4 = (289 * 1,732) / 4 = 125,137 cm
Ismeretes, hogy a bázis a piramis egy négyzet. Így egyértelmű, hogy ez a négy egyenlő oldalú háromszög. Ezután az oldalsó felülete a piramis a következőképpen számítjuk ki:
125.137 cm * 4 = 500,548 cm
A: palástfelületén a piramis 500.548 cm²
Először kiszámítjuk a területet az oldalsó felületén a piramis. Az oldalsó felületének köszönhetően a területének összege az összes oldalsó arcok. Ha foglalkozik a jobb piramis (vagyis egy, amelynek alapja egy szabályos sokszög és vertex kivetített közepén a sokszög), majd kiszámítja a teljes oldalsó felületén elegendő szaporodnak az alap kerülete (azaz az összeg a hossza minden oldalról a sokszög, ami fekszik a bázis piramis), hogy a magassága a oldalfelület (más néven apothem), és elosztjuk az eredményt 2: Sb = 1 / 2P * H, ahol Sb - egy oldalsó felülete, P - az alap kerületét, h - a magassága a oldalfelület (apothem).
Ha mielőtt önkényes piramis, meg kell külön területének kiszámítására az arcokon, majd verem őket. Mivel az oldalfelületek a piramis háromszögek, háromszög területén használja a következő képletet: S = 1 / 2b * H, ahol b - az alapja a háromszög, és a H - magassága. Ha a terület az arcokon számítjuk, az egyik csak add, hogy megkapja az oldalsó felülete a piramis.
Ezután meg kell számítani a területen az alapja a piramis. Kiválasztása a képlet számítási függ, amely sokszög rejlik az alapja a piramis: jobb (azaz, oly módon, hogy minden oldalról azonos hosszúságú) vagy helytelen. A terület egy szabályos sokszög lehet kiszámítani, hogy a kerülete által a sugara a sokszög kerülete, és elosztjuk az eredményt 2: Sn = 1 / 2P * r, ahol az SN - ez sokszögek területi, P - a kerülete, és r - a sugara a beírt sokszög kerülete .
Csonka gúla - poliéder, hogy egy piramist képeznek, és annak keresztmetszetét az alappal párhuzamos. Találja meg az oldalsó felülete csonka gúla egy pillanat alatt. A képlet nagyon egyszerű: a terület egyenlő a termék felének összege határain alapjainak apofemu. Tekintsük a példát a számítás terület a palástfelület egy csonka gúla. Tegyük adott rendszeres négyszögletes piramis. Hossza a bázis b = 5 cm, c = 3 cm. Apothem a = 4 cm. Ahhoz, hogy megtalálják a terület az oldalsó felületének egy piramis, először is meg kell találni a kerülete a bázisok. Egy nagy alapon lesz egyenlő p1 = 4b = 4 * 5 = 20 cm a kisebb alapja a képlet a következő: .. P2 = 4c = 4 * 3 = 12 cm Következésképpen, a terület lesz egyenlő: s = 1/2 (20 + 12 ) * 4 = 32/2 * 4 = 64 cm.
Ha a bázis a piramis egy szabálytalan sokszög, hogy kiszámolja a terület a teljes szám fog először meg kell osztani a sokszöget háromszögek, minden egyes kiszámított területen, majd hajtogatott. Más esetekben, hogy megtalálják a oldalfelületén a piramis, hogy megtalálják a terület minden egyes oldalfelületek és hajtsa ezeket az eredményeket. Bizonyos esetekben, a probléma megtalálásának oldalsó felületén a piramis lehet segíteni. Ha az egyik oldalsó felülete merőleges a bázis vagy két szomszédos oldala nézzen merőlegesek az alapra, a bázis a piramis részének tekintik a merőleges vetülete az oldalfelületén, és össze vannak kapcsolva a képletek.
A számítás elvégzéséhez, a felülete a piramis, a hajtogatott oldalú területet és az alapja a piramis.
Piramis - poliéder, amelyek közül az egyik néz (bázis) - tetszőleges sokszög, és a többi a (laterális) - háromszögek, amelyek közös csúcsa. Száma sarkokban a piramisok háromszög alakú alap (Tetrahedron), téglalap alakú, és így tovább.
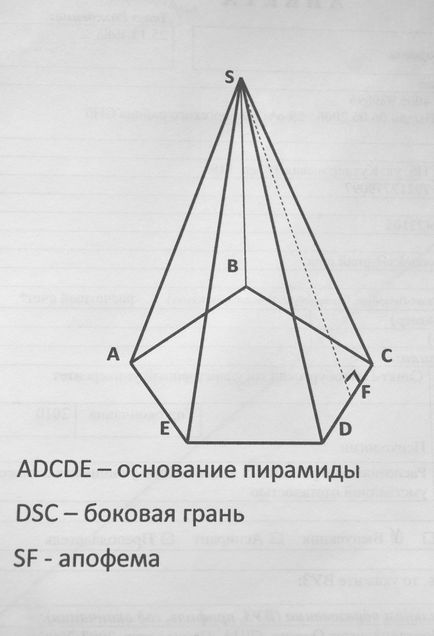
A piramis egy poliéder, amelynek egy bázis formájában egy sokszög, míg a fennmaradó arcok háromszögek egy közös csúcs. Apothem úgynevezett magassága a jobb oldalon arca a piramis, amely ki van húzva a csúcson.
A piramis egy poliéder, ami fekszik az alapja a sokszög, és az oldalsó arcok - ez háromszögek, amelyek közös csúcsa. Ploschadpoverhnostipiramidy egyenlő a négyzetösszeg oldalfelület és a bázis a piramis.
- Papír, toll, számológép
Először kiszámítjuk a területet az oldalsó poverhnostipiramidy. Az oldalsó felületének köszönhetően a területének összege az összes oldalsó arcok. Ha foglalkozik a jobb piramis (vagyis egy, amelynek alapja egy szabályos sokszög és vertex kivetített közepén a sokszög), majd kiszámítja a teljes oldalsó felületén elegendő szaporodnak az alap kerülete (azaz az összeg a hossza minden oldalról a sokszög, ami fekszik a bázis piramis), hogy a magassága a oldalfelület (más néven apothem), és elosztjuk az eredményt 2: Sb = 1 / 2P * H, ahol Sb - egy oldalsó felülete. P - az alap kerületét, h - a magassága a oldalfelület (apothem).
Ha mielőtt önkényes piramis, meg kell külön területének kiszámítására az arcokon, majd verem őket. Mivel az oldalfelületek a piramis háromszögek, háromszög területén használja a következő képletet: S = 1 / 2b * H, ahol b - az alapja a háromszög, és a H - magassága. Ha a terület összes arcok kerülnek kiszámításra, csak akkor tudjuk kombinálni őket, hogy a terület az oldalsó poverhnostipiramidy.
Ezután meg kell számítani a területen az alapja a piramis. Kiválasztása a képlet számítási függ, amely sokszög rejlik az alapja a piramis: jobb (azaz, oly módon, hogy minden oldalról azonos hosszúságú) vagy helytelen. A terület egy szabályos sokszög lehet kiszámítani, hogy a kerülete által a sugara a sokszög kerülete, és elosztjuk az eredményt 2: Sn = 1 / 2P * r, ahol az SN - ez sokszögek területi, P - a kerülete, és r - a sugara a beírt sokszög kerülete .
Ha az alapja a piramis egy szabálytalan sokszög, hogy ki lehessen számítani a terület az egész alakja újra meg kell törni a sokszög háromszögekre, számítani minden területen, majd dobott.
Hogy teljes legyen a számítás a terület poverhnostipiramidy. szeres területet a palástfelület és a bázis a piramis.