jellemző szilárdság

Az erő általában attól függ, az idő, a lényeg helyzetét és sebességét:

1. POWER, az idő függvényében:

Az elektromos térerősség olyan ponton elektromos töltés erő hat. Ha az elektromos térerősség függ az idő, a ható erő ponttöltés függ ideje:

Erői ebben az osztályban, de között ható anyag szervek közé, például motor alternáló mozgását a részek úgy hat, hogy az alapot. Sok esetben ezek az erők egy ismétlődő jellegét, és ezért úgy tűnik, hogy a trigonometrikus függvények.

2. POWER, attól csak a sebesség a lényeg:

Ezekkel erők mi leggyakrabban találkozunk, ha figyelembe vesszük a test mozgása egy rezisztens közegben. A teljesítmény a rezisztencia a részét a környezet csak akkor következik be, ha van mozgás a test képest a közeg. Ha a relatív sebessége nulla, az ellenállás erő eltűnik. Ezt az erőt a ellentétes irányú a test sebessége. ellenállási erő sebességétől függ a függőség az általános esetben összetett. Azonban a lassú mozgás a test relatív ellenállás erő arányos a sebesség:

ahol # 955; - az arányosság együttható tulajdonságaitól függően a közeg (abban az esetben a mozgás a testek # 955; Ez függ a alakja és méretei a szervezetben). Nagyobb sebességnél, ez a függés helytelen. Ebben az esetben van egy négyzetes vagy hidraulikus ellenállás joga:

ahol k - együttható arányosság függ ugyanazok a tényezők, mint ezt.

Nagyon nagy sebességgel, ez a törvény egyre bonyolultabbá vált, de egy megfelelő pontossággal lehet kiindulni, hogy az erő a mozgással szembeni ellenállást egy pont a folyadék vagy gáz csak attól függ, a sebesség és ellentétes irányban is.

FORCE, attól csak a pont pozícióját:

Különösen fontos, kétféle hatásköre ebben az osztályban: a rugalmas erő és a gravitációs erő.

a) a rugalmas erő

rugalmas erők során keletkező deformáció rugalmas testek. Egy példa a rugalmas erő lehet az erő eredő, amikor a rugó deformálódik. Amikor tavasszal a szabad állapotú - az erő nulla. De ha a rugó nyúlik, vagy csökken, ez lesz az az erő, amely megpróbálja vissza az eredeti állapotába.

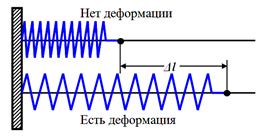
A tekercsrugó, ahol # 8710; l - nyúlás, k - arányossági tényező - tavaszi merevség együtthatóval.

| l | nem kötelező eleme a rugalmas erő (például feszítőtárcsákat ilyen függőség nem lineáris.) Azonban a legtöbb gyakorlati problémákat is figyelembe kell venni a rugalmas erő arányos a deformáció.

N rögzítési pont képest rögzített XYZ. - a sugár vektor az M pont hiányában deformáció a rugó - a sugár vektor az M pont jelenlétében a tavaszi deformáció. A rugalmas erő:

A „-” jel azt jelenti, hogy az erő ellentétes irányú a vektor.

Egy vektor egyenlet fejezi Hooke-törvény, ami a három egyenletet az előrejelzések:

Ha a pont helyzete M hiányában deformáció egybeesik a származási 0 a koordináta-rendszer, az előző egyenlet felírható:

Ha a szimmetria tengelye a tavaszi össze az egyik tengely a Descartes-féle koordináta-rendszer (például 0X tengely), megkapjuk az egydimenziós esetben a probléma:

b) a gravitációs erő

Gravitációs erő - erő által meghatározott egyetemes tömegvonzás törvénye. nyitott I. Newton (1678): a két anyag pont vonzzák egymást egy erő arányos a tömege az anyag pont és fordítottan arányos a távolság négyzetével közöttük:

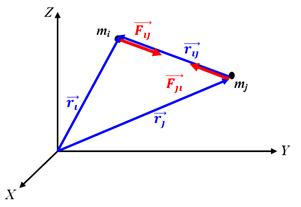
vagy, ahol - a vektor levonni a anyagi pont tömege mj az anyagi pont mi tömeget. - rádiuszvektorhoz tér által meghatározott helyzete a ponton, ahol a anyagi pont mi tömeget. - rádiuszvektorhoz tér által meghatározott helyzete a ponton, ahol a anyagi pont tömeget mj. = 6,67. 10-11 órán át. m2 / kg 2 - gravitációs állandó (első meghatározott 1798-ban Henry Cavendish).

Gravitációs erő kölcsönhatását a két anyag szervek viszonya határozza meg:

Minden téma ebben a szakaszban:

Mechanics - a tudomány és a mozgás egyensúlya szervek.
Kevesebb mechanikai mozgás megérteni változás abban a helyzetben szervek teret az idővel. Ismeri a mozgás tela-

Merev test - a test, a távolság bármely két pont között, amely során a mozgás változatlan marad.
A tér leírt euklideszi geometria. A legfontosabb tulajdonságai a tér - az egységesség (azonos tulajdonságai a tér a különböző területeken);

Speed ​​pont és jelenléte különböző módokon mozgás a lényeg
Az egyik fontos paraméter jellemzi, hogy a mozgás a mozgás sebessége pont. Úgy véljük, a mozgás a ponton, mivel a vektoros egyenletet e fogalom meghatározását:

Különös esetekben a pont
Egységes egyenes vonalú mozgás egyenletes egyenes vonalú mozgás van matematikailag meghatározott uravneniemNayde

Komplex mozgás egy pont
Mintegy test mozgásának ítélik mozgása által minden egyes pont. Korábban úgy gondoltuk, a mozgását egy pont a koordináta-rendszerben, amely hagyományosan vett rögzített. A gyakorlatban azonban, kell p

Transzlációs mozgása egy szilárd test
Mi először azt az egyszerű esetek mozgás - előre irányuló mozgás merev test és a merev test forgása.

Forgatás teljesen merev test körül rögzített tengely
Mi fix két pontot ATT. Gondoljunk bele, milyen nehéz, akkor az összes pontot, a test és megtanulják, hogyan kell meghatározni a sebességet és a Start

Forgatás egy merev test állandó szöggyorsulás
Lássuk, hogy ez a mozgás lesz írva, ha a kinematikai egyenlet a mozgás a test. Kezdetben kapunk egy képletet, amely lehetséges, hogy megtalálják a szögsebesség a test ebben az esetben. 0z Levél tengely mentén

Általános esetben a merev test mozgása
Megmutatjuk, hogy bármilyen mozgás merev test is képviselteti magát az összege a két mozgás: transzlációs és rotációs. Hagyja, hogy a test mozog önkényesen. Mi megkülönböztetni

kinetika
A tanuló a kinematikai mozgás testek megadottnak tekinti, és nem vagyunk érdekeltek az oka az oka, vagy a változás mozgást. Térjünk a tanulmány az okok meghatározására mechanikai

Anyagi pont tárolja a nyugalmi állapotban, illetve egységes egyenes vonalú mozgás, amíg amíg valamilyen erő nem fogja megváltoztatni ezt az állapotot.
Ez axióma kimondja, hogy a mozgás egy állandó nagysága és iránya a sebesség nem kell semmilyen hatalom. Ez a probléma nem korlátozódik a törvény a tehetetlenség. A törvény azt mondja, a béke, vagy

A mechanikus relativitás elve
Az egyenlet fejezi ki az alapvető jog dinamika világosan mutatja, hogy ez a törvény nem lehet igazságos bárki

részecske dinamika
Ennek alapján az axiómák a mechanika, dinamika alakul ki elsősorban a vizsgálat a második axióma, amelyet ezért nevezik alaptörvénye dinamikáját. Alaptörvénye dinamika van megfogalmazva egy

És a törvények a védelmi
Általános tételek a dinamikája anyagi pont logikus következménye az alaptörvény a dinamika testecskék. általában

A munkaerő. teljesítmény
Tegyük fel, hogy egy erő hat a mat

Tétel változás a kinetikus energia.
Tekintsük a mozgását egy pont hatására erő. A dinamikus egyenlete mozgás egy részecske felírható:

Törvény lendületmegmaradás a rendszer.
Tekintsük először a rendszer, amely a n tömeges pontok, amelyek mindegyike kölcsönhatásban más. Ezen túlmenően, az anyagi pont a rendszer működhet egy anyagi pont

Tétel a mozgás a tömegközéppontja
a tömegközéppontja vagy központ tehetetlenségi álló rendszer n tömeges pontok nevezzük geometriai pont, amelynek a helyzete a határozza meg a sugár vektor

A megmaradási törvénye impulzusmomentum mechanikai rendszer.
Nézzük először a rendszer, amely n anyagi pont. Írjunk alaptörvénye dinamikája az egyes pontokhoz:

A megmaradási törvénye teljes mechanikai energia a rendszer.
Írjunk alaptörvénye dinamikája az egyes pontokhoz. k = 1, 2, 3, ..., n. A skaláris szorzata ennek az egyenletnek n

DYNAMICS teljesen szilárd.
Önkényes merev test mozgása leírható két tételt - megváltoztatni a relatív perdület a tömegközéppont és a tétel a tömegközéppont mozgását.

Dinamikája transzlációs mozgása egy merev test.
Amikor az előre mozgó minden pontján merev test mozog azonos, így tudta, hogyan fog mozogni

A dinamikája szilárd test körüli forgás rögzített tengely.
A mozgási energia egy forgó merev test Először találunk egy kifejezés a kinetikus energia az anyag pont, forgatható szögsebesség

Az alapvető egyenlet a dinamika a rotációs mozgás
Hagyja, merev test körül forog rögzített tengely egybeesik a tengely 0z. A testület az aktív erő