Lineáris differenciálegyenlet másodrendű, példák, oldatok

Ebben a cikkben tartjuk alapelveit megtaláljuk a általános megoldások lineáris homogén és nem homogén másodrendű differenciálegyenletek, és részletesen elemezzük néhány példát a megoldásokat.

A homogén lineáris másodrendű differenciálegyenlet formájában, és egyenetlen, ahol az f (x). p (x) és a q (x) - a folyamatos intervallumon integráció X. A konkrét esetben, ahol a funkció p (x) = p és q (x) = Q jelentése állandó, találni egy általános megoldást szakaszban leírt homogén lineáris másodrendű differenciálegyenletek állandó együtthatós, inhomogén lineáris másodrendű differenciálegyenletek állandó együtthatók.

A mi kérik általános megoldásként Lineáris Közönséges differenciálegyenletek és LNDU másodrendű? Megfogalmazzuk két tétel, hogy válaszoljon erre a kérdésre.

Y0 általános megoldása a homogén lineáris differenciálegyenlet intervallumon X folyamatos együtthatóit X jelentése lineáris kombinációja n lineárisan független különösen oldatok Lineáris Közönséges differenciálegyenletek tetszőleges állandó együtthatók, azaz.

Az általános megoldása y inhomogén lineáris differenciálegyenlet intervallumban X folyamatos azonos időközzel együtthatók X és az f (x) az összege, ahol Y0 - az általános megoldás megfelelő lineáris Közönséges differenciálegyenletek, és - adott megoldást LNDU forrás.

• y0 = C1 ⋅y1 + C2 ⋅y2 - az általános megoldás a differenciálegyenlet, ahol Y1 és Y2 - annak lineárisan független különösen oldatok,
• és - az általános megoldás, ahol - valamely sajátos megoldások, és y0 - az általános megoldás a megfelelő lineáris Közönséges differenciálegyenletek.

Továbbra is megtanulják, hogyan kell megtalálni y1. és y2.

A legegyszerűbb esetben, ezek a funkciók kerülnek kiválasztásra.

Lineárisan független funkciók y1 és y2 közül a leggyakrabban állítja

A lineáris függetlenség funkciók y1 és y2 készülékkel ellenőrizzük a Wronskian. Ha a funkciók lineárisan függetlenek tartományban X. Wronski meghatározó nullától eltérő minden x intervallumban X.

Például, a funkciók y1 = 1 és Y2 = x lineárisan függetlenek bármely tényleges érték x. óta.

Funkció y1 = sinx és Y2 = cosx is lineárisan független a R. Mivel

De a funkció a y1 = - x - 1 és Y2 = x + 1 lineárisan függ az intervallum (-∞; + ∞). mert

Általánosságban, a kiválasztás y1. y2 és nehéz, és nem mindig lehetséges.

Ha felveszi egy nem triviális (nem nulla) y1 Lineáris Közönséges differenciálegyenletek másodrendű parciális megoldás, meg lehet találni egy általános megoldást, csökkenti a mértéke az egyenlet az első helyettesítéssel.

Find az általános megoldás egy homogén lineáris másodrendű differenciálegyenlet.

Ez könnyű észrevenni, hogy y1 = x egy adott megoldást a differenciálegyenlet x ≠ 0. Azt csökkenti a mértékét az eredeti egyenlet helyett a.

Ha felidézzük a szabály különbségtétel a termék tulajdonságainak és a határozatlan integrál. az

.

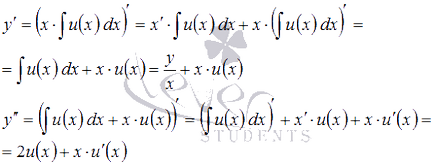
Behelyettesítve ezeket az eredményeket az eredeti egyenlet érkezünk a differenciálegyenlet több változó:

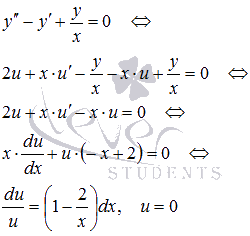
Integrálása mindkét oldalán, megkapjuk után potencírozódott általános megoldás felírható, ahol C - tetszőleges konstans.

Mivel feltételeztük, hogy az általános megoldás a kiindulási lineáris Közönséges differenciálegyenletek a másodrendű lesz, ahol F (x) függvény az egyik primitívek.

Primitív F (x) nem lehet kifejezni elemi funkcióit.

Megoldásában inhomogén lineáris másodrendű differenciálegyenlet, ha nem talál y1 és y2. nem tudja kezelni a kiválasztás. LNDU általános megoldás megtalálható a módszer variációs tetszőleges állandók.

Ebben az esetben, lineáris Közönséges differenciálegyenletek általános megoldás y0 = C1 ⋅ y1 + C2 ⋅ y2. Változó önkényes állandók, mint általános megoldások LNDU fogadja y0 = C1 (x) ⋅ y1 + C2 (x) ⋅ y2. Származékok ismeretlen függvények C1 (x) és C2 (x) határozzuk meg az egyenletrendszert, és a funkciók C1 (x) és C2 (x) kapott a későbbi integráció.

Find az általános megoldás az inhomogén lineáris másodrendű differenciálegyenlet.

Ez könnyű észrevenni, hogy a lineárisan független egyedi megoldásokat a megfelelő lineáris Közönséges differenciálegyenletek és, azaz a. Változtatása önkényes állandók, és általános megoldásként az eredeti differenciálegyenlet kerül.

Minősül egyenletrendszert

A probléma megoldása érdekében használjuk a módszert Cramer:

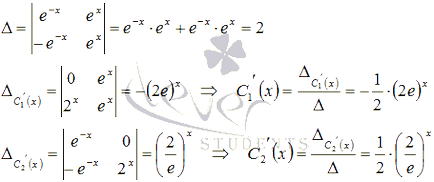
Integrálása a kapott kifejezések megtalálásához C1 (x) és C2 (x):

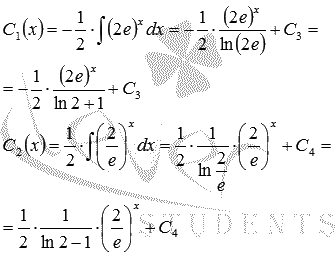
Így, az általános megoldás a kezdeti lineáris inhomogén differenciálegyenlet másodrendű a formája.

• Az általános megoldás a másodrendű lineáris Közönséges differenciálegyenletek törekedni y0 = C1 ⋅y1 + C2 ⋅y2. ahol y1 és y2 - a lineárisan független egyedi megoldásokat. Magán megoldások Y1 és Y2 a kiválasztott (általában ismert rendszer lineárisan független funkció). y1 és y2 választani nem mindig lehetséges, ezért találni általános megoldást a differenciálegyenlet nem mindig lehetséges. Ha csupán egyetlen megoldást y1 találtuk, a sorrendben az egyenlet lehet csökkenteni az első a változás által. Döntés a kapott egyenlet, általános megoldást a forrása a másodrendű lineáris Közönséges differenciálegyenletek.
• Az általános megoldás LNDU második kérelmei formájában, ahol - bármilyen részmegoldások belőle, és y0 - az általános megoldás megfelelő lineáris Közönséges differenciálegyenletek. Így, az első Y0 - az általános megoldás a differenciálegyenlet (ha lehetséges), akkor a kiválasztott (ha rendelkezésre áll). Vagy első kiválasztott y1 és y2 (ahogy szeretné), és LNDU általános megoldás határozza meg variációja tetszőleges állandók.

• Èl'sgol'ts LE Differenciálegyenletek és variációszámítás.