Mi egy paralelogramma, tulajdonságok, attribútumok, a terület egy paralelogramma

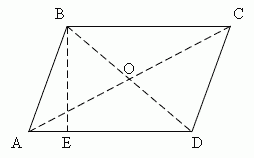
Paralelogramma (ógörög παραλληλόγραμμον származó παράλληλος -. Párhuzamos és γραμμή - line) - a négyszög, amelynek szemközti oldalai párhuzamosak, azaz hazugság párhuzamos vonalak. Különleges esetekben a paralelogramma egy négyzet és egy rombusz.

• paralelogramma szemközti oldalai egyenlő | AB | = | CD |. | AD | = | BC |.
• A szemközti szögek egy paralelogramma egyenlő
• paralelogramma átlói metszik egymást, és a metszéspont felezik | AO | = | OC |. | BO | = | OD |.
• A szögek összege szomszédos egyik oldalon 180.
• Bármilyen átlós osztja a paralelogramma-be 2 egyenlő háromszögek.
• A felezővonal frakcióknak a paralelogramma egyenlő szárú háromszög.
• A összessége szögek egyenlő 360 °
• A négyzetének összege a átlói paralelogramma kétszeresével egyenlő négyzetének összege a két szomszédos oldal:

hagyja, hogy egy - AB oldal hossza, b - oldal hossza BC, D1 és D2 - a hossza a átlók; majd

jelek egy paralelogramma

ABCD paralelogramma, ha az alábbi feltételeknek:

1. A szemközti oldalak egyenlő: AB = CD, AD = BC.
2. Szemközti szöge egyenlő: ∠A = ∠C, ∠B = ∠D.
3. Ezek osztva átlósan metszéspont a felére: AO = OC, BO = OD.
4. Összege szomszédos szögek 180 fok: ∠A + ∠B = 180, ∠B + ∠C = 180, ∠C + ∠D = 180, ∠D + ∠A = 180.
5. A szemközti oldalak egyenlő és párhuzamos: AB = CD, AB || CD-t.
6. A távolságok összege középpontjai közötti ellentétes oldalán egy konvex négyszög megegyezik annak semiperimeter.

A terület egy paralelogramma

. ahol egy - oldalán, h - magassága húzott erre az oldalra. Ahol a és b - oldalán, és α - oldalai közötti szög a és b