problémamegoldás algebrai módszer - matematika, előadások

Előadás a leckét a matematika 5 fokozatú, „Problémamegoldás algebrai módszer” tankönyv I.I.Zubarevoy. bemutatása célok:
- azt mutatják, általában problémamegoldás algebrai módszerrel;
- hogy létrehozzák a képességét, hogy megoldja a problémákat, a számtani és algebrai módszerek.

A példákban problémamegoldás № № 509 és 510, a tankönyv „matematika. Grade 5 „I.I.Zubarevoy tekinthető számtani és algebrai módszerek oldatot. Ha ezt a bemutatót az osztályban tanító lehet kérni a diákokat, hogy megtalálja a saját különböző módon megoldani a problémákat, majd kiegészíti a módszerek egy új módon - algebrai. Speciális hivatkozásokat előadást a hallgatók bizonyítani tudja a felvételi lehetőségek a problémák megoldására.

problémamegoldás algebrai módon (egyenletek) a könyv II Zubareva, AG Mordkovich

November matematika tanár „LSOSH №2»

Lihoslavl Tver régióban

Célok: - azt mutatják, általában algebrai problémamegoldó módon; -, hogy létrehozzák a képességét, hogy megoldja a problémákat, a számtani és algebrai módszerek.

Aritmetikai (a feladat a cselekvések)

Algebrai (megoldás a problémára segítségével az egyenlet)

Próbáld megtalálni különböző módon megoldásához.

A két doboz 16 kg cookie-kat. Keresse meg a máj súlya minden egyes dobozba, ha egy ilyen sütik 4 kg több, mint a másik.

1 módja, hogy megoldja

3 módon megoldani

2 módon megoldani

4 utat a megoldás

1 Eljárás (számtani)

• 16-4 = 12 (kg) - keksz marad a két doboz, kivéve, ha az első vezérlő egység 4 kg cookie-kat.

• 2 = 12. 6 (kg) - cookie volt a második mezőben.

• 6 + 4 = 10 (kg) - cookie volt az első mezőbe.

Válasz. keksz tömege az első doboz - 10 kg-os, és a második 6 kg.

A döntés, a korrekciós módszert.

Kérdésre. Ezért kapta a nevét?

2 módszer (számtani)

• 16 + 4 = 20 (kg) - cookie a két doboz, hozzátéve, 4 kg cookie-egy második doboz.

• 20 2 = 10 (kg) - cookie volt az első mezőbe.

• 10-4 = 6 (kg) - cookie volt a második mezőben.

Válasz. keksz tömege az első doboz - 10 kg-os, és a második 6 kg.

A döntés, a korrekciós módszert.

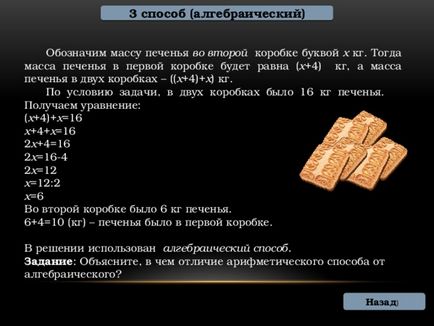
3. módszer (algebrai)

Jelöljük tészta tömege a második doboz által a levél x kg. Ezután a tészta tömegének az első doboz lesz egyenlő (x 4) kg, és cukrászati ​​masszát két doboz - ((4 x) + x) kg.

A feladat szerint, két doboz volt 16 kg keksz. Kapunk a következő egyenletet:

A második doboz 6 kg keksz.

6 + 4 = 10 (kg) - cookie volt az első mezőbe.

A döntés használt algebrai módszer.

Feladat. Mi a különbség a számtani az algebrai módszer?

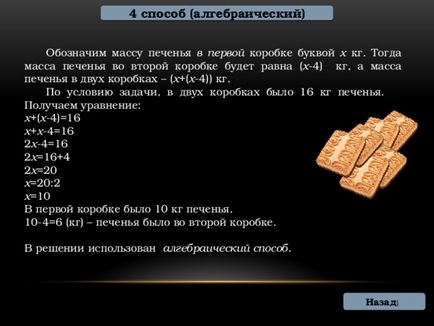
4. módszer (algebrai)

Jelöljük tészta tömege az első dobozt a levél x kg. Ezután a tömege tészta a második doboz egyenlő (x 4) kg, és cukrászati ​​masszát két doboz - (x + (x -4)) kg.

A feladat szerint, két doboz volt 16 kg keksz. Kapunk a következő egyenletet:

Az első doboz 10 kg cookie-kat.

10-4 = 6 (kg) - cookie volt a második mezőben.

A döntés használt algebrai módszer.

• Mi kétféleképpen a probléma megoldásának volna használni?
• Mi a módja a kiegyenlítés?
• Az első korrekciós módszert különbözik a második?
• Az egyik zseb 10 rubelt több, mint a másik. Hogyan lehet egyenlőségjelet az összeget mindkét zsebébe?
• Mi az algebrai módszer a probléma megoldásának?
• Mi különbözteti meg a 3 módon megoldani a problémát a 4.?
• Az egyik zseb 10 rubelt több, mint a másik. Köztudott, hogy egy kisebb összeget kijelölt változó x. Amint azt fejezzük ki x összeget a másik zsebében?
• Ha az x több pénzt a zsebében, míg lesz kifejezve x összeget a másik zsebében?
• Az üzlet sampon ára 25 rubel drágább, mint a szupermarketben. Kijelöl egy változót a levelet, és kifejezni a különböző költségek révén ez a változó.

Oldja meg a problémát számtani és algebrai módszerek.

Három telkek általuk összegyűjtött 156 mázsa burgonyát. Mivel az első és a második rész a burgonya gyűjtött egyformán, és a harmadik - 12 n értéke nagyobb, mint az egyes első két. Hány burgonyát gyűjtött parcellánként.

• 156-12 = 144 (c) - a burgonya volna gyűjtött három területen, ha a hozam az összes oldalak ugyanaz lenne.

• 144. 3 = 48 (n) - burgonya összegyűjtjük az első és a második kiemelkedő részei.
• 48 + 12 = 60 (p) - burgonya gyűjtött a harmadik rész.

Válasz. az első és a második rész 48 emelt n burgonyát, és egy harmadik része 60 ° C összegyűjtjük burgonya.

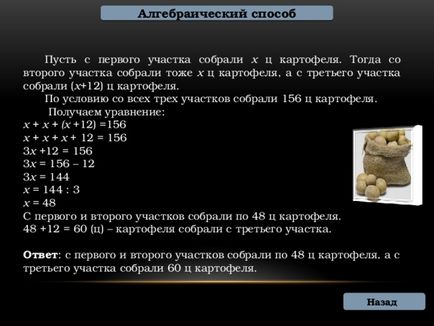
Tegyük fel, hogy az első rész összegyűjtjük x y burgonya. Ezután a második rész szintén összegyűjtjük burgonya x y, és a harmadik kiemelkedő rész (x 12) n burgonya.

By hipotézis, mindhárom webhely gyűjtött 156 mázsa burgonyát.

x + x + x + 12 = 156

Mivel az első és a második rész 48 emelt n burgonya.

48 + 12 = 60 (p) - burgonya gyűjtött a harmadik rész.

Válasz. az első és a második rész 48 emelt n burgonyát, és egy harmadik része 60 ° C összegyűjtjük burgonya.

Köszönöm a figyelmet