Az összeg és a termék teljes másodfokú egyenlet gyökerek, matematika-ismétlés

I. Wyeth-tétel a fenti másodfokú egyenlet.

Csökkentett összeg gyökerei a másodfokú egyenlet x 2 + px + q = 0 egyenlő a második együttható, hozott ellenkező előjelűek, és a termék a gyökerek egyenlő a konstans tag:

Keresse meg a gyökereket a fenti másodfokú egyenlet segítségével Térség tétel.

1. példa) x 2 -x-30 = 0. Ez vezetett másodfokú egyenlet (x 2 + px + q = 0). második együtthatójának p = -1. és az állandó kifejezés q = -30. Először győződjön meg arról, hogy az egyenletnek gyökerek és a gyökér (ha van) kell kifejezni az egész számokat. Elég, hogy a diszkrimináló volt tökéletes négyzet értéke.

Azt találjuk, a diszkrimináns D = b 2 - 4ac = (- 1) 1 2 -4 ∙ ∙ (-30) = 1 + 120 = 121 = 11 2.

Most, a tétel Térség összege a gyökereket meg kell egyeznie a második tényező, figyelni az ellenkező előjelű, azaz a (-p), és a termék megegyezik a konstans, azaz, (Q). majd:

Példa 2) x 2 + 6x + 8 = 0. Megadtuk másodfokú egyenlet egy második együtthatója p = 6 és q = szabad tag 8. Ügyeljen arra, hogy egész gyöke. Találunk a diszkrimináns D1. a második tényező - páros. D1 = -1 ∙ március 2 8 = 9-8 = 1 = 1 2. diszkrimináns D1 egy tökéletes négyzet száma 1. jelenti gyökerei az egyenlet egész számok. Mi vegye fel a gyökerei az Térség tétel: az összeg a gyökerek p = -6. és a termék a gyökerek egyenlő q = 8. Ez a szám a -2 és -4.

3. példa) x 2 + 2x-4 = 0. Ez a csökkentett másodfokú egyenlet második együttható p = 2. és az állandó kifejezés q = -4. Találunk a diszkrimináns D1. a második tényező - páros. D1 = február 1 -1 ∙ (-4) = 1 + 4 = 5. A diszkrimináns nem egy tökéletes négyzet számot, így arra lehet következtetni. A gyökerek az egyenlet nem egész számok, és megtalálni őket lehetetlen Térség tétel. Ezért, mi megoldja ezt a egyenletet, a szokásos módon, a képletek (ebben az esetben, a képletek az adott esetben még a második tényező). kapjuk:

4. példa). Készítsen egy másodfokú egyenlet annak gyökereit, ha x1 = -7, x2 = 4.

5. példa). Készíts egy másodfokú egyenlet annak gyökereit, ha:

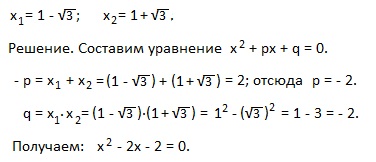
II. Wyeth-tétel teljes másodfokú egyenlet ax 2 + bx + c = 0.

gyökerek összege egyenlő mínusz b. osztva. termék a gyökerek egyenlő. osztva:

6. példa). Keresse meg az összeget a tér gyökerei az egyenlet 2x 2 -7x-11 = 0.

Úgy látjuk, hogy ez az egyenlet lesz gyökereit. Ez elég ahhoz, hogy azt a kifejezést diszkrimináló, és kiszámítása nélkül is, csak azért, hogy megbizonyosodjon arról, hogy a diszkrimináns nagyobb, mint nulla. D = 7 február -4 ∙ 2 ∙ (-11)> 0. Most használd teoremoyVieta teljes másodfokú egyenletek.

7. példa). Find a termék a gyökerek egy másodfokú egyenlet 3x 2 + 8x-21 = 0.

Oldal 1 1 1