Másodrendű differenciálegyenletek állandó együtthatós

Home | Rólunk | visszacsatolás

Másodrendű differenciálegyenlet állandó együtthatók formájában:

ha van egy nulla a jobb oldalon az egyenlet,

akkor az egyenlet nevezzük homogén lineáris.

Hogy oldja meg ezt az egyenletet készül a karakterisztikus egyenlet. A jellemző az úgynevezett másodfokú egyenlet kapott differenciálegyenlet, amelyben a helyettesitett új változó k, a mértéke által meghatározott sorrendben a-származék:

;

Ezután - a karakterisztikus egyenlet.

Találunk a gyökerei a karakterisztikus egyenlet:

1. Ha a karakterisztikus egyenletnek gyökerek valós és egyenlő. azaz deskremenant D = 0, a megoldás a differenciálegyenlet lesz a függvénye:

2. Ha a gyökerek karakterisztikus egyenlet valós és egyenlő számban. D> 0. akkor:

3. Ha a gyökerek a karakterisztikus egyenlet - komplex számok D<0, т.е. . то

Például: találni általános megoldást a differenciálegyenlet:

Azt, hogy ki a karakterisztikus egyenlet:

;

Találunk a gyökereihez:

;

Helyettesítse a kapott értéket a k = 1, (1) egyenlet, megkapjuk:

.

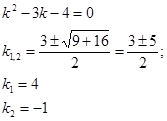
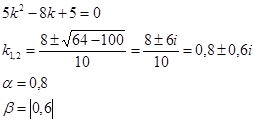
A kapott értékek # 945; és # 946; helyettesítő (3) egyenletet, megkapjuk:

5. A másodrendű differenciálegyenletek, hogy beengedje a közös csökkentő RENDELÉS

Tegyük fel, hogy egy differenciálegyenlet megoldott képest a második derivált:

,

Tekintsük a fajta másodrendű differenciálegyenletek, amelyek lehetővé teszik csökkentése érdekében:

I. differenciálegyenletek nem tartalmazzák az érv:

(*)

helyettesíteni ezt (*), kapjuk:

.

Kaptunk az elsőrendű differenciálegyenlet és a megoldás között lesz: vagy

Megosztott változók szorzataként mindkét oldalról:

.

Bevezetése szubsztitúció: (1)

Egyenlet (1) kapjuk: (2)

Behelyettesítve az értékeket egyenletek (1) és (3) egy előre meghatározott egyenletet, és kapjuk:

.

Kapott elsőrendű egyenletet. Megoldása Az elválasztási eljárás változók R és y. Az egyenlet megoldott tekintetében P.

.

Csökkentése mindkét fél által P

.

Osszuk a változók szorzataként mindkét fél kap:

.

Integrálja a két részből áll:

Helyettesítse a kapott értéket a következő egyenlet P (4) egyenletbe (1), kapjuk:

Visszanyerte elsőrendű differenciálegyenlet a változók y és x.

Osszuk a változók szorzataként mindkét oldalról. kapjuk:

.

Megkapjuk az általános megoldás a differenciálegyenlet:

II. Differenciálegyenletek nem tartalmazzák a szükséges funkció:

(**)

Ezután az egyenlet (**) lesz:

.

A megoldás ennek az egyenletnek a függvénye:

Bevezetése szubsztitúció: (1)

Behelyettesítve az értékeket egyenletek (1) és (2) az eredeti egyenlet és kapjuk:

.

Osszuk a változók szorzataként mindkét fél kap:

.

Integrálása a két oldalon az egyenlet:

Mi helyettesíti az F érték a (3) egyenletben a egyenlet (1), és szerezzen:

.

Osszuk a változók szorzataként mindkét oldalról. és integrálja:

III. A differenciálegyenletek, amely nem tartalmazza a funkciója ismeretlen és származéka:

(***)

Csere: helyettesítő (***)

Például: találni általános megoldást a differenciálegyenlet:

Bevezetése szubsztitúció: (1)

Behelyettesítve az értékek (2) egyenlet az eredeti egyenletet:

.

Osszuk a változók szorzataként mindkét oldalról kapjuk:

.

Egyenletet megoldva az integrálásával kaptunk két részből:

Helyettesítse az értéket az F a (3) egyenletben a (1) egyenlet, megkapjuk:

.

Osszuk a változók szorzataként mindkét oldalról. és integrálja:

.

Megjegyzés. Megoldása az integrál integrálásával szerint részből áll: