Spring 2 inga

Tavaszi inga egy anyagi pont tömege

, csatolt egy teljesen súlytalan elasztikus rugó merevsége . Két a legegyszerűbb esetben: a vízszintes (15. ábra, A) és függőleges (15. ábra, b) egy inga.

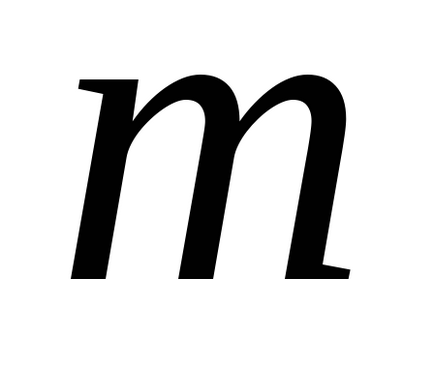
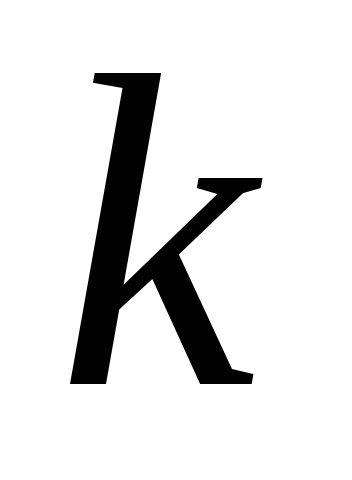
a) A vízszintes inga (ábra. 15a). eltolása rakomány

az egyensúlyi helyzetből értéke működik egy vízszintes napravleniivozvraschayuschaya rugalmas erő(Hooke-törvény).

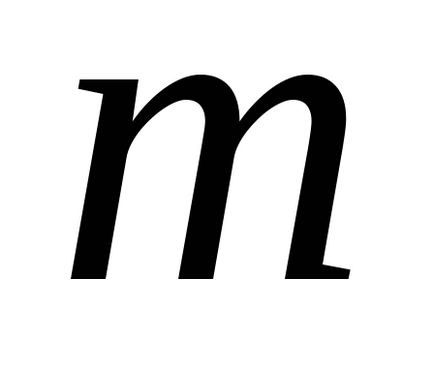
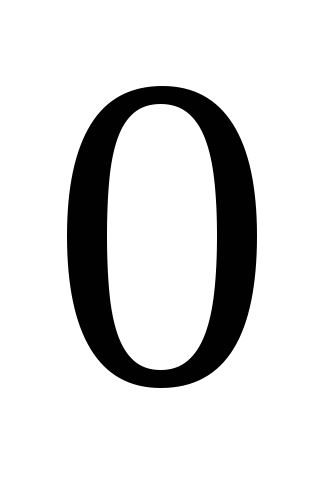
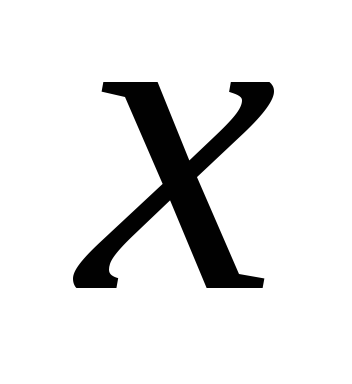
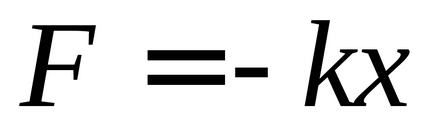
Feltételezzük, hogy a horizontális támogatás, amelyre a terhelés csúszda

ha annak rezgések teljesen sima (nincs súrlódás).

b) A függőleges inga (15. ábra, B). Az egyensúlyi helyzetben ebben az esetben az jellemzi, állapot:

ahol

- nagysága a rugalmas ható terhelés statikus feszültséget tavasszal alatt a gravitációs erő a terhelés.

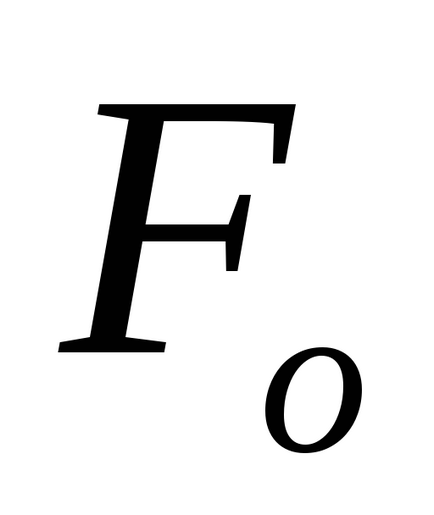
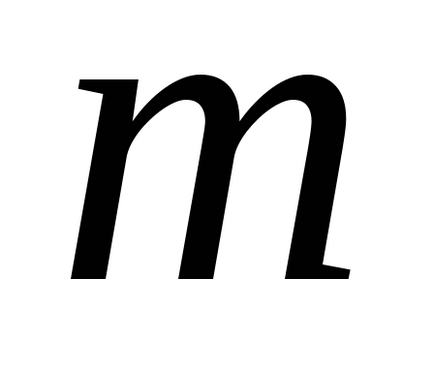
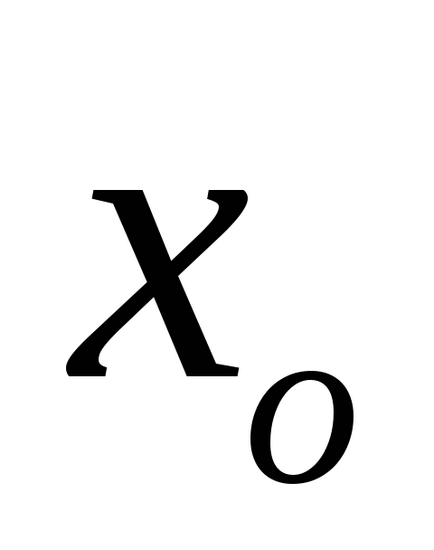
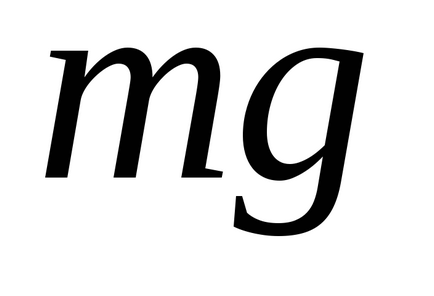
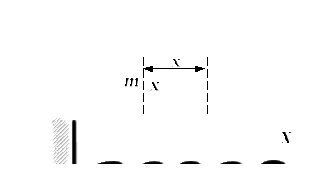
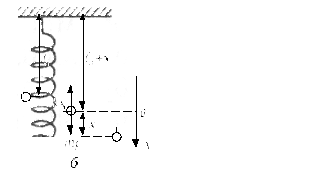
15. ábra. Tavaszi inga: a - b és vízszintes - függőleges

Ha nyúlik a rugó, és engedje el a terhelést, akkor kezdődik, hogy emelkedik. Ha az offset, hogy egy adott időpontban lesz

, A rugalmas erő most írva, mint egy.

Mindkét esetben a tavaszi inga leng egy időszak

és ciklusos gyakorisága

A példa a figyelmet a tavaszi inga, arra lehet következtetni, hogy a harmonikus rezgések - a mozgás okozta erő arányos az elmozdulás a növekvő

. Így, ha a visszaállító ereje hasonlít Hooke-törvény(Ő kapott nazvaniekvaziuprugoy erők), akkor a rendszernek kell végezni harmonikus rezgéseket. Abban az időben a folyosón egyensúlyi helyzetben a test nem a visszaállító erő hat, azonban a test tehetetlenségi túlhaladja az egyensúlyi helyzet és a visszaállító erőt megfordítja.

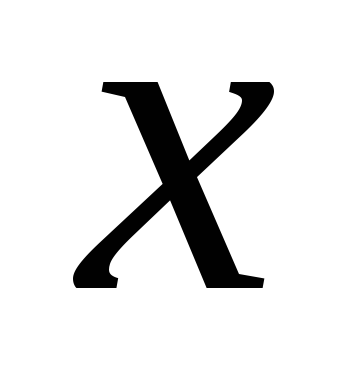
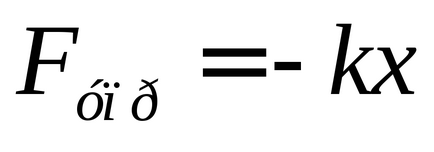
inga

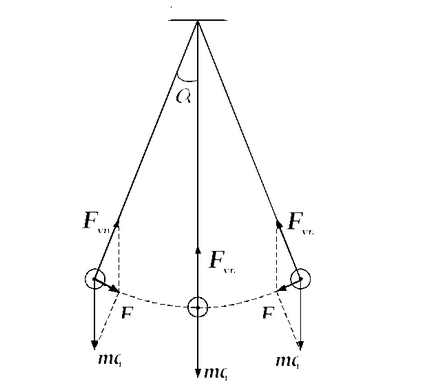
16. ábra. inga

Ingás jelentése idealizált rendszer formájában egy részecske szuszpendált egy súlytalan nyújthatatlan szál hossza

, alávetett kis rezgések a gravitáció (ábra. 16).

Variációk az inga kis szögek alakváltozás

(Legfeljebb 5 °) lehet tekinteni harmonikus, és a ciklusos gyakorisága matematikai inga:

2.3. test energia harmonikus rezgések

Az energia adódik át a rezgő rendszer kezdeti lökést adott időközönként átalakítja a potenciális energia a rugó deformálódik, hogy beköltözik kinetikus energia mozgó rakomány és vissza.

Let tavasszal inga leng a kezdeti fázisban

, azaz(Ábra17).

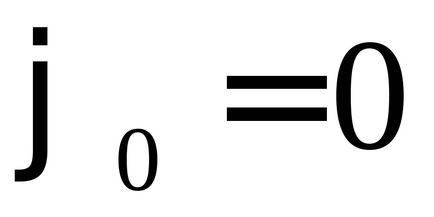
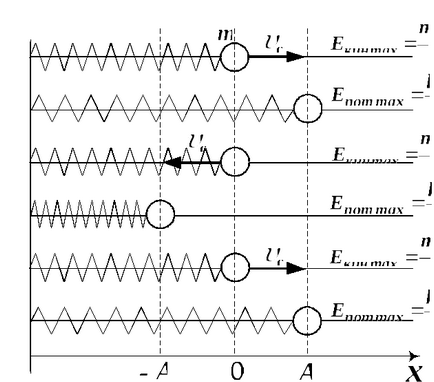
17. ábra. A törvény a mechanikai energia megmaradás

A rezgések a tavaszi inga

A maximális terhelés eltérése az egyensúlyi helyzetből az inga teljes mechanikai energia (az energia egy deformált rugó merevsége

) az . Amikor elhaladnak az egyensúlyi helyzet (), A potenciális energia a tavaszi nullává válik, és a teljes mechanikai energia a rezgő rendszer úgy definiáljuk, mint .

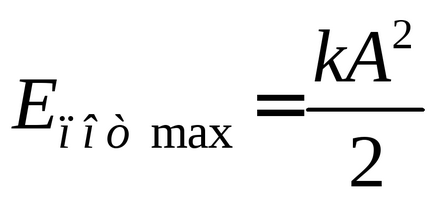
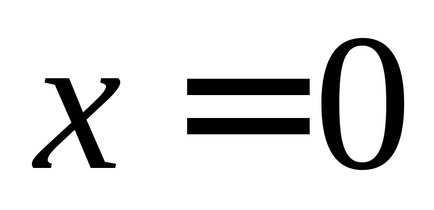
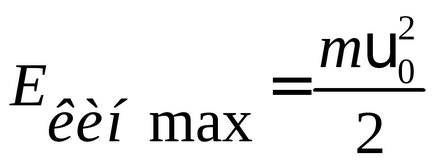
18. ábra grafikonjai a kinetikus függőségek, a potenciális, és a teljes energia, ha a harmonikus rezgéseket leírt trigonometrikus szinusz függvény (szaggatott vonal), vagy cosinus (folytonos vonal).

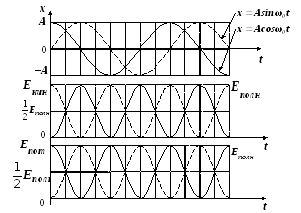
18. ábra. Grafikonok az idő függvényében kinetikus

és a potenciális energia harmonikus rezgések

A grafikonok (ábra18), hogy a frekvencia variációs a kinetikus és a potenciális energia kétszerese természetes frekvenciája a harmonikus rezgések.