Vertex (geometria)

A szög csúcspontját - ez az a pont, Okuda származnak két gerenda.

A szög csúcspontját - ez az a pont, ahol a két gerenda származnak; ahol a két szegmens konvergálnak; Ahol a két vonal metszi; ahol bármely kombinációja gerendák és egyenes szegmenseket alkotó két (egyszerű) „oldal”, hogy konvergálnak egy pontban [2].

poliéder sokszög

Csúcs - a sarokpont a sokszög vagy poliéder (bármely méretben), más szóval a 0-dimenziós arcokat.

A sokszög csúcsa az úgynevezett „konvex”, ha a szög kisebb, mint a belső sokszög π radián (180 ° - két derékszögben). Ellenkező esetben a vertex az úgynevezett „konkáv”.

Általánosabban, a csúcsa a poliéder egy konvex poliéder, ha metszéspontja egy kellően kis területen. amelynek csúcsa, mint a központ, ez egy konvex alakúak; egyébként, a vertex konkáv.

Csúcsai a poliéder társított a gráf. mivel a poliéder egy olyan grafikon, amelynek csúcsai megfelelnek a csúcsai a poliéder [3]. és így, a grafikon a poliéder lehet tekinteni, mint egy-dimenziós simplicial komplex. amelynek csúcsai a a gráf. Azonban a csúcsok gráfelmélet lehet legalább két incidens élek. ami általában nem megengedett geometriai csúcsok. Van egy kapcsolat a geometriai csúcsok és a csúcsok a görbe. görbülete szélsőértékek pontokat - a sokszög csúcsait a bizonyos értelemben pont végtelen görbületét, és ha a poligon közelíthető egy sima görbe, pontok szélsőséges görbület közel esik a sokszög csúcsainak [4]. Azonban, egy közelítése sokszög segítségével a sima görbe ad további csúcsot pontok minimális görbületi.

Lapos tetők mozaikok

Vertex sík mozaik (csempék) - ez az a pont, ahol három vagy több gyűrűt mozaik [5]. de nem kizárólagosan: a csempe csempék is sokszögek és mozaik felsők a tetejét ezeket a lapokat. Általánosabban, cserép lehet tekinteni, mint egyfajta topológiai CW-komplexum. A tetejét a más típusú rendszerek, mint például simplicial. - ez a közeljövőben a nulla dimenzió.

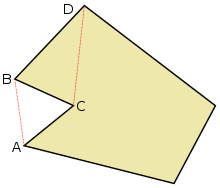
Vertex B „fül”, mint egy nyitott intervallum közötti csúcsok a C és D fekszik teljesen a sokszög belsejében. Vertex C „száj”, mint egy nyitott intervallum A és B között fekszik teljesen kívül a sokszög.

Vertex x i> egyszerű P sokszög az elsődleges csúcs, ha az átlós [x i - 1 x i + 1], x _]> P keresztezi határokat csak pontok x i - 1>, és x i + 1>. Két alaptípusa csúcsok: „fülek” és a „száját” (lásd alább). [6].

A fő csúcs a x i> egy egyszerű P sokszög az úgynevezett "száj", ha az átlós [x i - 1 x i + 1], x _]> kívül fekszik, P.

A csúcsok száma a poliéder

ahol V - a csúcsok száma, E - az élek számát, és F - az arcok száma. Ez az egyenlet az úgynevezett Euler-egyenlet. Például cube 12 hat arcok és élek, és ezért - 8 csúcsa: 8 - 12 + 2 = 6.

Csúcsok számítógépes grafika

A számítógépes grafika tárgyak gyakran képviselteti magát a Triangulated poliéder. amelyben a csúcsok a tárgy összehasonlítjuk a nem csak a három térbeli koordinátákat. hanem más szükséges a megfelelő képalkotó a tárgy grafikus információkat, mint például a szín, fényvisszaverő. textúra. vertex normals [7]. Ezeket a tulajdonságokat a használt konstrukció a képet egy vertex shader. Néhány top felvezető [en].